1. Math Problem Solving Methods
2. Help Solving Math Word Problems
3. Math Problem Solving Strategies
4. Math Problem Solving Chapter 5 Lesson 6
5. Solving Math Word Problems Free

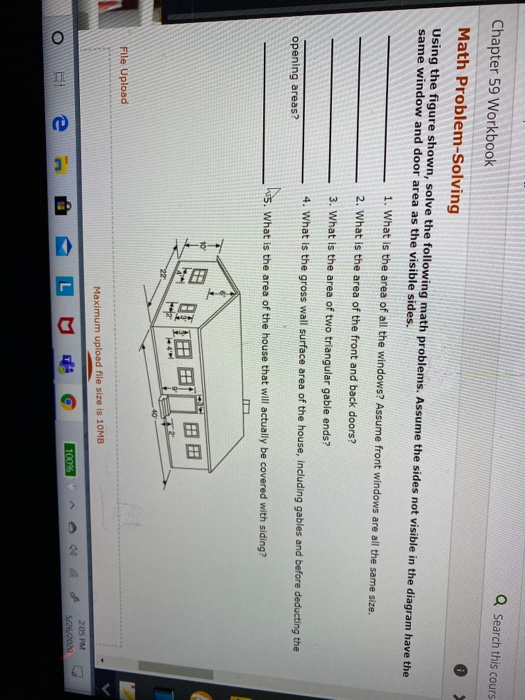
The Mathematical Reasoning & Problem-Solving chapter of this Contemporary Math: Help & Review course is the simplest way to master reasoning and problem-solving in math. And problems for the concept exercises in each lesson.The exercises are designed to aid your study of mathematics by reinforcing important mathematical skills needed to succeed in the everyday world.The materials are organized by chapter and lesson, with one Word Problem Practice worksheetfor every lesson in Glencoe Math Connects, Course 2. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. Math & Problem Solving Chapter Exam Instructions. Choose your answers to the questions and click 'Next' to see the next set of questions. You can skip questions if you would like and come back to.

Classzone.com has been retired and is no longer accessible. Because of the age of this application, the programs supported by this platform are not able to benefit from the technological improvements in accessibility, security, and HMTL5 (non-Flash) that we have incorporated into our newer programs and platforms in recent years.

Learn more about HMH's newest classroom solutions.

If you want to retrieve your user data from the platform that is no longer accessible, please contact techsupport@hmhco.com or 800.323.9239 and let us know that you're contacting us about user data extraction from Classzone.com.

Please note, user data extraction does not include program content.

Across content areas, the standards address problem-solving in the form of being able to improvise, decide, inquire, and research. In fact, math and science standards are premised almost completely on problem-solving and inquiry. According to the literature, however, problem-solving and inquiry are often overlooked or addressed only superficially in classrooms, and in some subject areas, are not attended to at all.

OVERVIEW OF PROBLEM-SOLVING AND INQUIRY IN K–12 CLASSROOMS

In keeping with a learning focus, this chapter first discusses problem-solving and inquiry to provide a basis from which teachers can provide support for these goals with technology.

What Is Problem-solving?

Whereas production is a process that focuses on an end-product, problem-solving is a process that centers on a problem. Students apply critical and creative thinking skills to prior knowledge during the problem-solving process. The end result of problem-solving is typically some kind of decision, in other words, choosing a solution and then evaluating it.

There are two general kinds of problems. Close-ended problems are those with known solutions to which students can apply a process similar to one that they have already used. For example, if a student understands the single-digit process in adding 2 plus 2 to make 4, she most likely will be able to solve a problem that asks her to add 1 plus 1. Open-ended or loosely structured problems, on the other hand, are those with many or unknown solutions rather than one correct answer. These types of problems require the ability to apply a variety of strategies and knowledge to finding a solution. For example, an open-ended problem statement might read:

A politician has just discovered information showing that a statement he made to the public earlier in the week was incorrect. If he corrects himself he will look like a fool, but if he doesn’t and someone finds out the truth, he will be in trouble. What should he do or say about this?

Obviously, there is no simple answer to this question, and there is a lot of information to consider.

Many textbooks, teachers, and tests present or ask only for the results of problem-solving and not the whole process that students must go through in thinking about how to arrive at a viable solution. As a result, according to the literature, most people use their personal understandings to try to solve open-ended problems, but the bias of limited experience makes it hard for people to understand the trade-offs or contradictions that these problems present. To solve such problems, students need to be able to use both problem-solving skills and an effective inquiry process.

What Is Inquiry?

Inquiry in education is also sometimes called research, investigation, or guided discovery. During inquiry, students ask questions and then search for answers to those questions. In doing so, they come to new understandings in content and language. Although inquiry is an instructional strategy in itself, it is also a central component of problem-solving when students apply their new understandings to the problem at hand. Each question that the problem raises must be addressed by thorough and systematic investigation to arrive at a well-grounded solution. Therefore, the term “problem-solving” can be considered to include inquiry.

For students to understand both the question and ways of looking at the answer(s), resources such as historical accounts, literature, art, and eyewitness experiences must be used. In addition, each resource must be examined in light of what each different type of material contributes to the solution. Critical literacy, or reading beyond the text, then, is a fundamental aspect of inquiry and so of problem-solving. Search for critical literacy resources by using “critical literacy” and your grade level, and be sure to look at the tools provided in this text’s Teacher Toolbox.

What Is Problem-Based Learning?

Problem-based learning (PBL) is a teaching approach that combines critical thinking, problem- solving skills, and inquiry as students explore real-world problems. It is based on unstructured, complex, and authentic problems that are often presented as part of a project. PBL addresses many of the learning goals presented in this text and across the standards, including communication, creativity, and often production.

Research is being conducted in every area from business to education to see how we solve problems, what guides us, what information we have and use during problem-solving, and how we can become more efficient problem solvers. There are competing theories of how people learn to and do solve problems, and much more research needs to be done. However, we do know several things. First, problem-solving can depend on the context, the participants, and the stakeholders. In addition, studies show that content appears to be covered better by “traditional” instruction, but students retain better after problem-solving. PBL has been found effective at teaching content and problem-solving, and the use of technology can make those gains even higher (Chauhan, 2017). Research clearly shows that the more parts of a problem there are, the less successful students will be at solving it. However, effective scaffolding can help to support students’ problem-solving and overcomes some of the potential issues with it (Belland, Walker, Kim, & Lefler, 2017).

The PBL literature points out that both content knowledge and problem-solving skills are necessary to arrive at solutions, but individual differences among students affect their success, too. For example, field-independent students in general do better than field-dependent students in tasks. In addition, students from some cultures will not be familiar with this kind of learning, and others may not have the language to work with it. Teachers must consider all of these ideas and challenges in supporting student problem-solving.

Characteristics of effective technology-enhanced problem-based learning tasks

PBL tasks share many of the same characteristics of other tasks in this book, but some are specific to PBL. Generally, PBL tasks:

Involve learners in gaining and organizing knowledge of content. Inspiration and other concept-mapping tools like the app Popplet are useful for this.

Help learners link school activities to life, providing the “why” for doing the activity.

Give students control of their learning.

Have built-in and just-in-time scaffolding to help students. Tutorials are available all over the Web for content, language, and technology help.

Are fun and interesting.

Contain specific objectives for students to meet along the way to a larger goal.

Have guidance for the use of tools, especially computer technologies.

Include communication and collaboration (described in chapter 3).

Gms vst download. Emphasize the process and the content.

Are central to the curriculum, not peripheral or time fillers.

Math Problem Solving Methods

Lead to additional content learning.

Have a measurable, although not necessarily correct, outcome.

More specifically, PBL tasks:

Use a problem that “appeals to human desire for resolution/stasis/harmony” and “sets up need for and context of learning which follows” (IMSA, 2005, p. 2).

Help students understand the range of problem-solving mechanisms available.

Focus on the merits of the question, the concepts involved, and student research plans.

Provide opportunities for students to examine the process of getting the answer (for example, looking back at the arguments).

Lead to additional “transfer” problems that use the knowledge gained in a different context. Notice board .

Not every task necessarily exhibits all of these characteristics completely, but these lists can serve as guidelines for creating and evaluating tasks.

Student benefits of problem-solving

There are many potential benefits of using PBL in classrooms at all levels; however, the benefits depend on how well this strategy is employed. With effective PBL, students can become more engaged in their learning and empowered to become more autonomous in classroom work. This, in turn, may lead to improved attitudes about the classroom and thus to other gains such as increased abilities for social-problem solving. Students can gain a deeper understanding of concepts, acquire skills necessary in the real world, and transfer skills to become independent and self-directed learners and thinkers outside of school. For example, when students are encouraged to practice using problem-solving skills across a variety of situations, they gain experience in discovering not only different methods but which method to apply to what kind of problem. Furthermore, students can become more confident when their self-esteem and grade does not depend only on the specific answer that the teacher wants. In addition, during the problem-solving process students can develop better critical and creative thinking skills.

Students can also develop better language skills (both knowledge and communication) through problems that require a high level of interaction with others (Verga & Kotz, 2013). This is important for all learners, but especially for ELLs and others who do not have grade-level language skills. For students who may not understand the language or content or a specific question, the focus on process gives them more opportunities to access information and express their knowledge.

The problem-solving process

The use of PBL requires different processes for students and teachers. The teacher’s process involves careful planning. There are many ways for this to happen, but a general outline that can be adapted includes the following steps:

After students bring up a question, put it in the greater context of a problem to solve (using the format of an essential question; see chapter 4) and decide what the outcome should be–a recommendation, a summary, a process?

Develop objectives that represent both the goal and the specific content, language, and skills toward which students will work.

List background information and possible materials and content that will need to be addressed. Get access to materials and tools and prepare resource lists if necessary.

Write the specific problem. Make sure students know what their role is and what they are expected to do. Then go back and check that the problem and task meet the objectives and characteristics of effective PBL and the relevant standards. Reevaluate materials and tools.

Develop scaffolds that will be needed.

Evaluate and prepare to meet individual students’ needs for language, assistive tools, content review, and thinking skills and strategies

Present the problem to students, assess their understanding, and provide appropriate feedback as they plan and carry out their process.

The student process focuses more on the specific problem-solving task. PBL sources list different terms to describe each step, but the process is more or less the same. Students:

Define and frame the problem: Describe it, recognize what is being asked for, look at it from all sides, and say why they need to solve it.

Plan: Present prior knowledge that affects the problem, decide what further information and concepts are needed, and map what resources will be consulted and why.

Inquire: Gather and analyze the data, build and test hypotheses.

Look back: Review and evaluate the process and content. Ask “What do I understand from this result? What does it tell me?”

These steps are summarized in Figure 6.1.

Problem-solving strategies that teachers can demonstrate, model, and teach directly include trial and error, process of elimination, making a model, using a formula, acting out the problem, using graphics or drawing the problem, discovering patterns, and simplifying the problem (e.g., rewording, changing the setting, dividing it into simpler tasks). Even the popular KWL (Know, Want to Know, Learned) chart can help students frame questions. A KWL for a project asking whether a superstore should be built in the community might look like the one in Figure 6.2. Find out more about these strategies at http://literacy.kent.edu/eureka/strategies/discuss-prob.html.

Teaching problem-solving in groups involves the use of planning and other technologies. Using these tools, students post, discuss, and reflect on their joint problem-solving process using visual cues that they create. This helps students focus on both their process and the content. Throughout the teacher and student processes, participants should continue to examine cultural, emotional, intellectual, and other possible barriers to problem-solving.

Teachers and Problem-solving

The teacher’s role in PBL

During the teacher’s process of creating the problem context, the teacher must consider what levels of authenticity, complexity, uncertainty, and self-direction students can access and work within. Gordon (1998) broke loosely structured problems into three general types with increasing levels of these aspects. Still in use today, these are:

Academic challenges. An academic challenge is student work structured as a problem arising directly from an area of study. It is used primarily to promote greater understanding of selected subject matter. The academic challenge is crafted by transforming existing curricular material into a problem format.

Scenario challenges. These challenges cast students in real-life roles and ask them to perform these roles in the context of a reality-based or fictional scenario.

Real-life problems. These are actual problems in need of real solutions by real people or organizations. They involve students directly and deeply in the exploration of an area of study. And the solutions have the potential for actual implementation at the classroom, school, community, regional, national, or global level. (p. 3)

To demonstrate the application of this simple categorization, the learning activities presented later in this chapter follow this outline.

As discussed in other chapters in this book, during student work the teacher’s role can vary from director to shepherd, but when the teacher is a co-learner rather than a taskmaster, learners become experts. An often-used term for the teacher’s role in the literature about problem-solving is “coach.” As a coach, the teacher works to facilitate thinking skills and process, including working out group dynamics, keeping students on task and making sure they are participating, assessing their progress and process, and adjusting levels of challenge as students’ needs change. Teachers can provide hints and resources and work on a gradual release of responsibility to learners.

Challenges for teachers

For many teachers, the roles suggested above are easier said than done. To use a PBL approach, teachers must break out of the content-dissemination mode and help their students to do the same. Even when this happens, in many classrooms students have been trained to think that problem-solving is getting the one right answer, and it takes time, practice, and patience for them to understand otherwise. Some teachers feel that they are obligated to cover too much in the curriculum to spend time on PBL or that using real-world problems does not mesh well with the content, materials, and context of the classroom. However, twenty years ago Gordon (1998) noted, “whether it’s a relatively simple matter of deciding what to eat for breakfast or a more complex one such as figuring out how to reduce pollution in one’s community, in life we make decisions and do things that have concrete results. Very few of us do worksheets” (p. 2). He adds that not every aspect of students’ schoolwork needs to be real, but that connections should be made from the classroom to the real world. Educators around the world are still working toward making school more like life.

In addition, many standardized district and statewide tests do not measure process, so students do not want to spend time on it. However, teachers can overcome this thinking by demonstrating to students the ways in which they need to solve problems every day and how these strategies may transfer to testing situations.

Furthermore, PBL tasks and projects may take longer to develop and assess than traditional instruction. However, teachers can start slowly by helping students practice PBL in controlled environments with structure, then gradually release them to working independently. The guidelines in this chapter address some of these challenges.

GUIDELINES FOR TECHNOLOGY-SUPPORTED PROBLEM-SOLVING

Obviously, PBL is more than simply giving students a problem and asking them to solve it. The following guidelines describe other issues in PBL.

Designing Problem-Solving Opportunities

The guidelines described here can assist students in developing a PBL opportunity.

Guideline #1: Integrate reading and writing. Although an important part of solving problems, discussion alone is not enough for students to develop and practice problem-solving skills. Effective problem-solving and inquiry require students to think clearly and deeply about content, language, and process. Reading and writing tasks can encourage students to take time to think about these issues and to contextualize their thinking practice. They can also provide vehicles for teachers to understand student progress and to provide concrete feedback. Students who have strengths in these areas will be encouraged and those who need help can learn from their stronger partners, just as those who have strengths in speaking can model for and assist their peers during discussion. Even in courses that do not stress reading and writing, integrating these skills into tasks and projects can promote successful learning.

Guideline #2: Avoid plagiarism. The Internet is a great resource for student inquiry and problem-solving. However, when students read and write using Internet resources, they often cut and paste directly from the source. Sometimes this is an innocent mistake; students may be uneducated about the use of resources, perhaps they come from a culture where the concept of ownership is completely different than in the United States, or maybe their language skills are weak and they want to be able to express themselves better. In either case, two strategies can help avoid plagiarism: 1) The teacher can teach directly about plagiarism and copyright issues. Strategies including helping students learn how to cite sources, paraphrase, summarize, and restate; 2) The teacher can be as familiar as possible with the resources that students will use and check for plagiarism when it is suspected. To do so, the teacher can enter a sentence or phrase into any Web browser with quote marks around it and if the entry is exact, the original source will come up in the browser window. Essay checkers such as Turnitin (http://turnitin.com/) are also available online that will check a passage or an entire essay.

Guideline #3: Do not do what students can do. Teaching, and particularly teaching with technology, is often a difficult job, due in part to the time it takes teachers to prepare effective learning experiences. Planning, developing, directing, and assessing do not have to be solely the teacher’s domain, however. Students should take on many of these responsibilities, and at the same time gain in problem-solving, language, content, critical thinking, creativity, and other crucial skills. Teachers do not always need to click the mouse, write on the whiteboard, decide

criteria for a rubric, develop questions, decorate the classroom, or perform many classroom and learning tasks. Students can take ownership and feel responsibility. Although it is often difficult for teachers to give up some of their power, the benefits of having more time and shared responsibility can be transformational. Teachers can train themselves to ask, “Is this something students can do?”

Guideline #4: Make mistakes okay. Problem-solving often involves coming to dead ends, having to revisit data and reformulate ideas, and working with uncertainty. For students used to striving for correct answers and looking to the teacher as a final authority, the messiness of problem-solving can be disconcerting, frustrating, and even scary. Teachers can create environments of acceptance where reasoned, even if wrong, answers are recognized, acknowledged, and given appropriate feedback by the teacher and peers. Teachers already know that students come to the task with a variety of beliefs and information. In working with students’ prior knowledge, they can model how to be supportive of students’ faulty ideas and suggestions. They can also ask positive questions to get the students thinking about what they still need to know and how they can come to know it. They can both encourage and directly teach students to be supportive of mistakes and trials as part of their team-building and leadership skills.

In addition, teachers may need to help students to understand that even a well-reasoned argument or answer can meet with opposition. Students must not feel that they have made a bad decision just because everyone else, particularly the teacher, does not agree. Teachers can model for students that they are part of the learning process and they are impartial as to the outcome when the student’s position has been well defended.

PROBLEM-SOLVING AND INQUIRY TECHNOLOGIES

As with all the goals in this book, the focus of technology in problem-solving is not on the technology itself but on the learning experiences that the technology affords. Different tools exist to support different parts of the process. Some are as simple as handouts that students can print and complete, others as complex as modeling and visualization software. Many software tools that support problem-solving are made for experts in the field and are relatively difficult to learn and use. Examples of these more complicated programs include many types of computer-aided design software, advanced authoring tools, and complex expert systems. In the past there were few software tools for K–12 students that addressed the problem-solving process directly and completely, but more apps are being created all the time that do so. See the Teacher Tools for this text for examples.

Simple inquiry tools that help students perform their investigations during PBL are much more prevalent. The standard word processor, database, concept mapping/graphics and spreadsheet software can all assist students in answering questions and organizing and presenting data, but there are other tools more specifically designed to support inquiry. Software programs that can be used within the PBL framework are mentioned in other chapters in this text. These programs, such as the Tom Snyder Productions/Scholastic programs mentioned in chapter 2 address the overlapping goals of collaboration, production, critical thinking, creativity, and problem-solving. Interestingly, even video games might be used as problem-solving tools. Many of these games require users to puzzle out directions, to find missing artifacts, or to follow clues that are increasingly difficult to find and understand. One common tool with which students at all levels might be familiar is Minecraft (Mojang; https://minecraft.net/en-us/). The Internet has as many resources as teachers might need to use Minecraft across the disciplines to teach whole units and even gamify the classroom.

The following section presents brief descriptions of tools that can support the PBL process. The examples are divided into stand-alone tools that can be used on one or more desktops and Web-based tools.

Stand-Alone Tools

Example 1: Fizz and Martina’s Math Adventures (Tom Snyder Productions/Scholastic)

Students help Fizz and Martina, animated characters in this software, to solve problems by figuring out which data is relevant, performing appropriate calculations, and presenting their solutions. The five titles in this series are perfect for a one-computer classroom. Each software package combines computer-based video, easy navigation, and handouts and other resources as scaffolds. This software is useful in classrooms with ELLs because of the combination of visual, audio, and text-based reinforcement of input. It is also accessible to students with physical disabilities because it can run on one computer; students do not have to actually perform the mouse clicks to run the software themselves.

This software is much more than math. It includes a lot of language, focuses on cooperation and collaboration in teams, and promotes critical thinking as part of problem-solving. Equally important, it helps students to communicate mathematical ideas orally and in writing. See Figure 6.6 for the “getting started” screen from Fizz and Martina to view some of the choices that teachers and students have in using this package.

Example 2: I Spy Treasure Hunt, I Spy School Days, I Spy Spooky Mansion (Scholastic)

The language in these fun simulations consists of isolated, discrete words and phrases, making these programs useful for word study but not for overall concept learning. School Days, for example, focuses on both objects and words related to school. However, students work on extrapolation, trial and error, process of elimination, and other problem-solving strategies. It is difficult to get students away from the computer once they start working on any of the simulations in this series. Each software package has several separate hunts with a large number of riddles that, when solved, allow the user to put together a map or other clues to find the surprise at the end. Some of the riddles involve simply finding an item on the screen, but others require more thought such as figuring out an alternative representation for the item sought or using a process of elimination to figure out where to find it. All of the riddles are presented in both text and audio and can be repeated as many times as the student requires, making it easier for language learners, less literate students, and students with varied learning preferences to access the information. Younger students can also work with older students or an aide for close support so that students are focused. Free versions of the commercial software and similar types of programs such as escape rooms (e.g., escapes at 365 Escape {http://www.365escape.com/Room-Escape-Games.html] and www.primarygames.com) can be found across the Web.

There are many more software packages like these that can be part of a PBL task. See the Teacher Toolbox for ideas.

Example 3: Science Court (Tom Snyder Productions/Scholastic)

Twelve different titles in this series present humorous court cases that students must help to resolve. Whether the focus is on the water cycle, soil, or gravity, students use animated computer-based video, hands-on science activities, and group work to learn and practice science and the inquiry process. As students work toward solving the case, they examine not only the facts but also their reasoning processes. Like Fizz and Martina and much of TSP’s software, Science Court uses multimedia and can be used in the one-computer classroom (as described in chapter 2), making it accessible to diverse students.

Example 4: Geographic Information Systems (GIS)

The use of GIS to track threatened species, map hazardous waste or wetlands in the community, or propose solutions for other environmental problems supports student “spatial literacy and geographic competence” (Baker, 2005, n.p.), in addition to experimental and inquiry techniques, understanding of scale and resolution, and verification skills. Popular desktop-based GIS that students can access include Geodesy and ArcVoyager; many Web-based versions also exist. A GIS is not necessarily an easy tool to learn or use, but it can lead to real-world involvement and language, concept, and thinking skills development.

Web-Based Tools

Many technology-enhanced lessons and tools on the Web come premade. In other words, they were created for someone else’s students and context. Teachers must adapt these tools to fit their own teaching styles, student needs, goals, resources, and contextual variables. Teachers must learn to modify these resources to make them their own and help them to work effectively in their unique teaching situation. With this in mind, teachers can take advantage of the great ideas in the Web-based tools described below.

Example 1: WebQuest

A WebQuest is a Web-based inquiry activity that is highly structured in a preset format. Most teachers are aware of WebQuests—a Web search finds them mentioned in every state, subject area, and grade level, and they are popular topics at conferences and workshops. Created by Bernie Dodge and Tom March in 1995 (see http://webquest.org/), this activity has proliferated wildly.

Each WebQuest has six parts. The Quest starts with an introduction to excite student interest. The task description then explains to students the purpose of the Quest and what the outcome will be. Next, the process includes clear steps and the scaffolds, including resources, that students will need to accomplish the steps. The evaluation section provides rubrics and assessment guidelines, and the conclusion section provides closure. Finally, the teacher section includes hints and tips for other teachers to use the WebQuest.

Advantages to using WebQuests as inquiry and problem-solving tools include:

Students are focused on a specific topic and content and have a great deal of scaffolding.

Students focus on using information rather than looking for it, because resources are preselected.

Students use collaboration, critical thinking, and other important skills to complete their Quest.

Teachers across the United States have reported significant successes for students participating in Quests. However, because Quests can be created and posted by anyone, many found on the Web do not meet standards for inquiry and do not allow students autonomy to work in authentic settings and to solve problems. Teachers who want to use a WebQuest to meet specific goals should examine carefully both the content and the process of the Quest to make sure that they offer real problems as discussed in this chapter. A matrix of wonderful Quests that have been evaluated as outstanding by experts is available on the site.

Although very popular, WebQuests are also very structured. This is fine for students who have not moved to more open-ended problems, but to support a higher level of student thinking, independence, and concept learning, teachers can have students work in teams on Web Inquiry Projects (http://webinquiry.org/).

Example 2: Virtual Field Trips

Virtual field trips are great for concept learning, especially for students who need extra support from photos, text, animation, video, and audio. Content for field trips includes virtual walks through museums, underwater explorations, house tours, and much more (see online field trips suggested by Steele-Carlin [2014] at http://www.educationworld.com/a_tech/tech/tech071.shtml). However, the format of virtual field trips ranges from simple postcard-like displays to interactive video simulations, and teachers must review the sites before using them to make sure that they meet needs and goals.

With a virtual reality headset (now available for sale cheaply even at major department stores), teachers and students can go on Google Expeditions (https://edu.google.com/expeditions/), 3D immersive field trips from Nearpod (http://nearpod.com), and even create their using resources from Larry Ferlazzo’s “Best Resources for Finding and Creating Virtual Field Trips” at http://larryferlazzo.edublogs.org/2009/08/11/the-best-resources-for-finding-and-creating-virtual-field-trips/.

Example 3: Raw Data Sites

Raw data sites abound on the Web, from the U.S. Census to the National Climatic Data Center, from databases full of language data to the Library of Congress. These sites can be used for content learning and other learning goals. Some amazing sites can be found where students can collect their own data. These include sites like John Walker’s (2003) Your Sky (www.fourmilab.to/yoursky) and Water on the Web (2005, waterontheweb.org). When working with raw data students have to draw their own conclusions based on evidence. This is another important problem-solving skill. Note that teachers must supervise and verify that data being entered for students across the world is accurate or

Example 4: Filamentality

Filamentality (https://keithstanger.com/filamentality.html) presents an open-ended problem with a lot of scaffolding. Students and/or teachers start with a goal and then create a Web site in one of five formats that range in level of inquiry and problem-solving from treasure hunts to WebQuests. The site provides lots of help and hints for those who need it, including “Mentality Tips” to help accomplish goals. It is free and easy to use, making it accessible to any teacher (or student) with an Internet connection.

Example 5: Problem Sites

Many education sites offer opportunities for students to solve problems. Some focus on language (e.g., why do we say “when pigs fly”?) or global history (e.g., what’s the real story behind Tut’s tomb?); see, for example, the resources and questions in The Ultimate STEM Guide for Students at http://www.mastersindatascience.org/blog/the-ultimate-stem-guide-for-kids-239-cool-sites-about-science-technology-engineering-and-math/. These problems range in level from very structured, academic problems to real-world unsolved mysteries.

The NASA SciFiles present problems in a format similar to WebQuests at https://knowitall.org/series/nasa-scifiles. In other parts of the Web site there are video cases, quizzes, and tools for problem-solving.

There is an amazing number of tools, both stand-alone and Web-based, to support problem-solving and inquiry, but no tool can provide all the features that meet the needs of all students. Most important in tool choice is that it meets the language, content, and skills goals of the project and students and that there is a caring and supportive teacher guiding the students in their choice and use of the tool.

Teacher Tools

There are many Web sites addressed specifically to teachers who are concerned that they are not familiar enough with PBL or that they do not have the tools to implement this instructional strategy. For example, from Now On at http://www.fno.org/toolbox.html provides specific suggestions for how to integrate technology and inquiry. Search “problem-solving” on the amazing Edutopia site (https://www.edutopia.org/) for ideas, guidelines, examples, and more.

LEARNING ACTIVITIES: PROBLEM-SOLVING AND INQUIRY

In addition to using the tools described in the previous section to teach problem-solving and inquiry, teachers can develop their own problems according to the guidelines throughout this chapter. Gordon’s (1998) scheme of problem-solving levels (described previously)—academic, scenario, and real life—is a simple and useful one. Teachers can refer to it to make sure that they are providing appropriate structure and guidance and helping students become independent thinkers and learners. This section uses Gordon’s levels to demonstrate the variety of problem-solving and inquiry activities in which students can participate. Each example is presented with the question/problem to be answered or solved, a suggestion of a process that students might follow, and some of the possible electronic tools that might help students to solve the problem.

Academic problems

Example 1: What Will Harry Do? (Literature)

Problem: At the end of the chapter, Harry Potter is faced with a decision to make. What will he do?

Process: Discuss the choices and consequences. Choose the most likely, based on past experience and an understanding of the story line. Make a short video to present the solution. Test it against Harry’s decision and evaluate both the proposed solution and the real one.

Tools: Video camera and video editing software.

Example 2: Treasure Hunt (History)

Problem: Students need resources to learn about the Civil War.

Process: Teacher provides a set of 10 questions to find specific resources online.

Tools: Web browser.

Example 3: Problem of the Week (Math)

Problem: Students should solve the math problem of the week.

Process: Students simplify the problem, write out their solution, post it to the site for feedback, then revise as necessary.

Tools: Current problems from the Math Forum@Drexel, http://mathforum.org/pow/

Scenarios

Example 1: World’s Best Problem Solver

Problem: You are a member of a committee that is going to give a prestigious international award for the world’s best problem-solver. You must nominate someone and defend your position to the committee, as the other committee members must do.

Process: Consult and list possible nominees. Use the process of elimination to determine possible nominees. Research the nominees using several different resources. Weigh the evidence and make a choice. Prepare a statement and support.

Help Solving Math Word Problems

Tools: Biography.com has over 25,000 biographies, and Infoplease (infoplease.com) and the Biographical Dictionary (http://www.s9.com/) provide biographies divided into categories for easy searching.

Example 2: Curator

Problem: Students are a committee of curators deciding what to hang in a new community art center. They have access to any painting in the world but can only hang 15 pieces in their preset space. Their goals are to enrich art appreciation in the community, make a name for their museum, and make money.

Process: Students frame the problem, research and review art from around the world, consider characteristics of the community and other relevant factors, choose their pieces, and lay them out for presentation to the community.

Tools: Art museum Web sites, books, and field trips for research and painting clips; computer-aided design, graphics, or word processing software to lay out the gallery for viewing.

Example 3: A New National Anthem

Problem: Congress has decided that the national anthem is too difficult to remember and sing and wants to adopt a new, easier song before the next Congress convenes. They want input from musicians across the United States. Students play the roles of musicians of all types.

Process: Students define the problem (e.g., is it that “The Star-Spangled Banner” is too difficult or that Congress needs to be convinced that it is not?). They either research and choose new songs or research and defend the current national anthem. They prepare presentations for members of Congress.

Tools: Music sites and software, information sites on the national anthem.

Real-life problems

Example 1: Racism in School

Problem: There have been several incidents in our school recently that seem to have been racially motivated. The principal is asking students to consider how to make our school a safe learning environment for all students.

Process: Determine what is being asked—the principal wants help. Explore the incidents and related issues. Weigh the pros and cons of different solutions. Prepare solutions to present to the principal.

Tools: Web sites and other resources about racism and solutions, graphic organizers to organize the information, word processor or presentation software for results. Find excellent free tools for teachers and students at the Southern Poverty Law Center’s Teaching Tolerance Web site at www.tolerance.org.

Example 2: Homelessness vs. Tpagetamizhfriends az songs. Education

Problem: The state legislature is asking for public input on the next budget. Because of a projected deficit, political leaders are deciding which social programs, including education and funding for the homeless, should be cut and to what extent. They are interested in hearing about the effects of these programs on participants and on where cuts could most effectively be made.

Process: Decide what the question is (e.g., how to deal with the deficit? How to cut education or funding for the homeless? Which programs are more important? Something else?). Perform a cost-benefit analysis using state data. Collect other data by interviewing and researching. Propose and weigh different solution schemes and propose a suggestion. Use feedback to improve or revise.

Tools: Spreadsheet for calculations, word processor for written solution, various Web sites and databases for costs, electronic discussion list or email for interviews.

Example 3: Cleaning Up

Problem: Visitors and residents in our town have been complaining about the smell from the university’s experimental cattle farms drifting across the highway to restaurants and stores in the shopping center across the street. They claim that it makes both eating and shopping unpleasant and that something must be done.

Process: Conduct onsite interviews and investigation. Determine the source of the odor. Measure times and places where the odor is discernible. Test a variety of solutions. Choose the most effective solution and write a proposal supported by a poster for evidence.

Tools: Online and offline sources of information on cows, farming, odor; database to organize and record data; word processing and presentation software for describing the solution.

These activities can all be adapted and different tools and processes used. As stated previously, the focus must be both on the content to be learned and the skills to be practiced and acquired. More problem-solving activity suggestions and examples can be found at site at http://www.2learn.ca/.

ASSESSING LEARNER PROBLEM-SOLVING AND INQUIRY

Many of the assessments described in other chapters of this text, for example, rubrics, performance assessments, observation, and student self-reflection, can also be employed to assess problem-solving and inquiry. Most experts on problem-solving and inquiry agree that schools need to get away from testing that does not involve showing process or allowing students to problem-solve; rather, teachers should evaluate problem-solving tasks as if they were someone in the real-world context of the problem. For example, if students are studying an environmental issue, teachers can evaluate their work throughout the project from the standpoint of someone in the field, being careful that their own biases do not cloud their judgment on controversial issues. Rubrics, multiple-choice tests, and other assessment tools mentioned in other chapters of this text can account for the multiple outcomes that are possible in content, language, and skills learning. These resources can be used as models for assessing problem-solving skills in a variety of tasks. Find hundreds of problem-solving rubrics by searching the Web for “problem-solving rubrics” or check Pinterest for teacher-created rubrics.

In addition to the techniques mentioned above, many teachers suggest keeping a weekly problem-solving notebook (also known as a math journal or science journal), in which students record problem solutions, strategies they used, similarities with other problems, extensions of the problem, and an investigation of one or more of the extensions. Using this notebook to assess students’ location and progress in problem-solving could be very effective, and it could even be convenient if learners can keep them online as a blog or in a share cloud space.

FROM THE CLASSROOM

Research and Plagiarism

We’ve been working on summaries all year and the idea that copying word for word is plagiarism. When they come to me (sixth grade) they continue to struggle with putting things in their own words so [Microsoft Encarta] Researcher not only provides a visual (a reference in APA format) that this is someone else’s work, but allows me to see the information they used to create their report as Researcher is an electronic filing system. It’s as if students were printing out the information and keeping it in a file that they will use to create their report. But instead of having them print everything as they go to each individual site they can copy and paste until later. When they finish their research they come back to their file, decide what information they want to use, and can print it out all at once. This has made it easier for me because the students turn this in with their report. So, I would say it not only allows students to learn goals of summarizing, interpreting, or synthesizing, it helps me to address them in greater depth and it’s easier on me! (April, middle school teacher)

WebQuests

I evaluated a WebQuest for middle elementary (third–fourth grades), although it seems a little complicated for that age group. The quest divides students into groups and each person in the group is given a role to play (a botanist, museum curator, ethnobotanist, etc.). The task is for students to find out how plants were used for medicinal purposes in the Southwest many years ago. Students then present their findings, in a format that they can give to a national museum. Weird. It was a little complicated and not well done. I liked the topic and thought it was interesting, but a lot of work would need to be done to modify it so that all students could participate. (Jennie, first-grade teacher).

CHAPTER REVIEW

Key Points

Define problem-solving and inquiry.

The element that distinguishes problem-solving or problem-based learning from other strategies is that the focal point is a problem that students must work toward solving. A proposed solution is typically the outcome of problem-solving. During the inquiry part of the process, students ask questions and then search for answers to those questions.

Math Problem Solving Strategies

Understand the interaction between problem-solving and other instructional goals. Although inquiry is also an important instructional strategy and can stand alone, it is also a central component of problem-solving because students must ask questions and investigate the answers to solve the problem. In addition, students apply critical and creative thinking skills to prior knowledge during the problem-solving process, and they communicate, collaborate, and often produce some kind of concrete artifact.

Discuss guidelines and tools for encouraging effective student problem-solving.

It is often difficult for teachers to not do what students can do, but empowering students in this way can lead to a string of benefits. Other guidelines, such as avoiding plagiarism, integrating reading and writing, and making it okay for students to make mistakes, keep the problem-solving process on track. Tools to assist in this process range from word processing to specially designed inquiry tools.

Create and adapt effective technology-enhanced tasks to support problem-solving. Teachers can design their own tasks following guidelines from any number of sources, but they can also find ready-made problems in books, on the Web, and in some software pack-ages. Teachers who do design their own have plenty of resources available to help. A key to task development is connecting classroom learning to the world outside of the classroom.

Assess student technology-supported problem-solving.

In many ways the assessment of problem-solving and inquiry tasks is similar to the assessment of other goals in this text. Matching goals and objectives to assessment and ensuring that students receive formative feedback throughout the process will make success more likely.

REFERENCES

Baker, T. (2005). The history and application of GIS in education. KANGIS: K12 GIS Community. Available from http://kangis.org/learning/ed_docs/gisNed1.cfm.

Belland, B., Walker, A., Kim, N., & Lefler, M. (2017). Synthesizing results from empirical research on computer-based scaffolding in STEM education: A meta-analysis. Review of Educational Research, 87(2), pp. 309-344.

Chauhan, S. (2017). A meta-analysis of the impact of technology on learning effectiveness of elementary students. Computers & Education, 105, pp. 14-30.

Dooly, M. (2005, March/April). The Internet and language teaching: A sure way to interculturality? ESL Magazine, 44, 8–10.

Gordon, R. (1998, January).Balancing real-world problems with real-world results. Phi Delta Kappan, 79(5), 390–393. [electronic version]

Math Problem Solving Chapter 5 Lesson 6

IMSA (2005). How does PBL compare with other instructional approaches? Available: http://www2.imsa.edu/programs/pbln/tutorials/intro/intro7.php.

Molebash, P., & Dodge, B. (2003). Kickstarting inquiry with WebQuests and web inquiry projects. Social Education, 671(3), 158–162.

Solving Math Word Problems Free

Verga, L., & Kotz, S. A. (2013). How relevant is social interaction in second language learning? Frontiers in Human Neuroscience, 7, 550. http://doi.org/10.3389/fnhum.2013.00550